논리학입문 제2장 논증의 분석

Fig.1 Book cover

논증의 패러프레이징

논증의 패러프레이징은 일상 생활에서의 문장을 논증의 형태로 알기 쉽도록 다시 풀어 쓰는 것을 의미한다. 교과서에서는 다음과 같은 예시를 든다.

"언어의 생명은 끝이 있고, 수학적 개념은 영원하기 때문에, 비극 시인 아이스킬로스가 우리의 기억에서 사라질지라도 아르키메데스는 기억될 것이다."

위 문장은 아래와 같이 패러프레이징할 수 있다.

1. 언어의 생명은 끝이 있다.
2. 아이스킬로스의 희곡들은 언어로 쓰여 있다.
3. 그러므로 아이스킬로스의 작품은 결국 사라질 것이다.
4. 수학적 개념은 영원하다.
5. 아르키메데스의 작품들은 수학적 관념으로 되어 있다.
6. 그러므로 아르키메데스의 작품들은 결코 사라지지 않을 것이다.
7. 따라서 아이스킬로스가 우리의 기억에서 사라질지라도, 아르키메데스는 기억될 것이다.

논증의 다이어그램

논증은 다이어그램을 통해 분석될 수 있다. 각 논증에 번호를 붙이고, 그 논증 간 관계를 배치와 화살표를 통해 나타내는 것이다. 각 논증이 서로 대등하다면 수평 위치에, 각 논증이 서로 전제-결론 관계라면 위-아래에 화살표를 통해 표시된다.

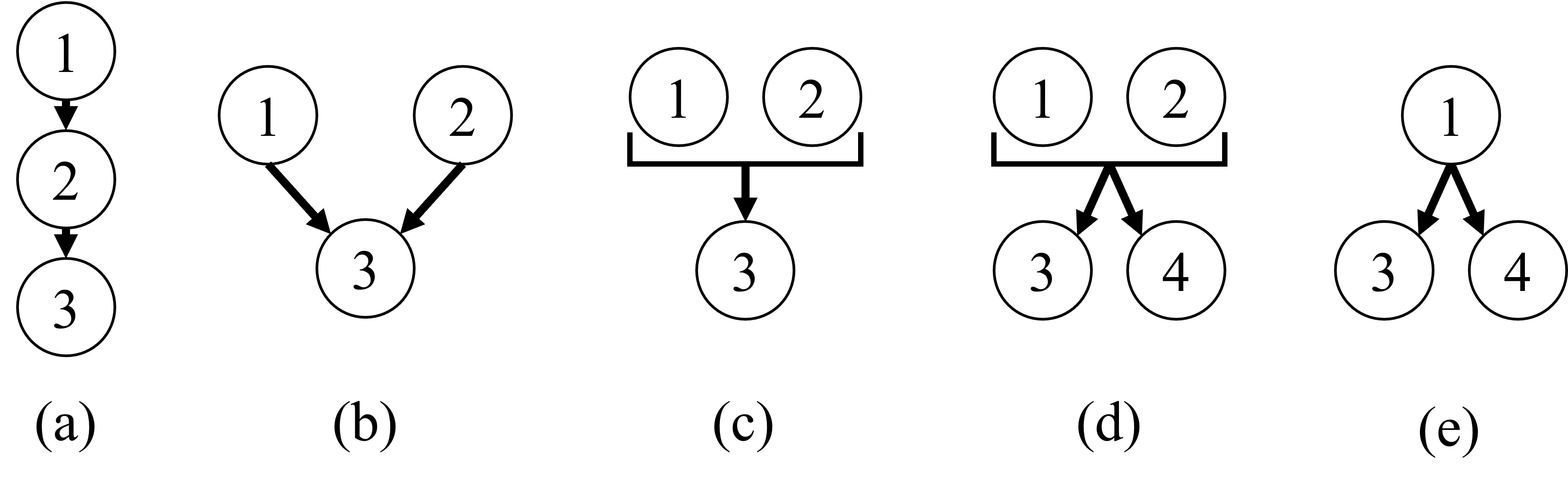
Fig.2 Examples of the logic diagram

그림 2.(a)의 다이어그램은 두 전제가 서로 다른 위치에서 전제-결론의 관계로 뒷받침하고 있다. 아래와 같은 예시를 생각해 볼 수 있겠다.

1. 교수는 대학원생의 목표인 졸업의 결정권을 가지고 있다.
2. 그러므로 대학원생은 교수의 의사를 거절하기 힘든 위치에 있다.
3. 그러므로 교수와 대학원생은 완전히 상하 관계에 있다.

그림 2.(b)의 다이어그램은 두 전제가 서로 동등한 위치에 있고, 같은 결론을 낸다. 아래와 같은 예시를 생각해 볼 수 있겠다.

1. 대학원생은 야근을 시켰을 때 인간보다 더 오래 버틸 수 있다.
2. 대학원생은 인간보다 적은 휴가를 주어도 더 오래 버틸 수 있다.
3. 그러므로 대학원생은 인간보다 인내심이 높은 아종이다.

그림 2.(c)의 다이어그램은 두 전제가 동등한 위치에서 서로 협력하여 결론을 뒷받침하고 있다. 그림 2.(b)와 다른 점은, (b)에서는 각 전제가 별개로 결론을 뒷받침할 수 있다. 즉, 1→3, 2→3만 생각해도 논증이 성립된다. 하지만 (c)에서는 두 전제 중 하나가 없으면 결론이 성립할 수 없다. 아래 예시를 보자.

1. 인간은 교수가 바늘로 찔렀을 때 도망을 쳤다.
2. 대학원생은 교수가 바늘로 찔러도 도망을 치지 않았다.
3. 그러므로 대학원생은 교수가 바늘로 찔렀을 때 인간보다 더 큰 인내심을 가진다.

위 예시의 결론은 대학원생과 인간을 비교하고 있다. 때문에 1번 전제만으로는 3번 결론을 가질 수 없고, 마찬가지로 2번 전제만으로는 3번 결론을 가질 수 없다. 오직 1-2번 전제가 같이 있어야만 3번 결론을 가질 수 있기 때문에, 다이어그램에서 괄호를 통해 표현되어야만 한다.

한 글에서 여러 결론이 있을 수도 있다. 그림 2.(d)의 다이어그램은 두 전제가 협력하여 두 결론을 뒷받침하고 있다.

1. 인간은 교수가 바늘로 찔렀을 때 도망을 쳤다.
2. 대학원생은 교수가 바늘로 찔러도 도망을 치지 않았다.
3. 교수는 인간과 대학원생을 바늘로 찌를 수 있다.
4. 대학원생은 교수가 바늘로 찔렀을 때 인간보다 더 큰 인내심을 가진다.

또는 그림 2.(e)와 같이 한 전제가 두 결론을 가질 수도 있다.

1. 연차가 높은 대학원생은 오랜 기간 졸업을 위한 한 분야의 연구에 매진해 왔다.
2. 연차가 높은 대학원생은 모진 시련에도 연구실을 옮기기 어렵다.
3. 연차가 높은 대학원생은 모진 시련에도 대학원을 그만두기 어렵다.

복잡한 논증적인 글들

일상 생활에서의 문장은 앞서 소개한 다양한 다이어그램처럼 단순한 구조를 가지기보다는, 복합적으로 엮인 형태를 가질 수 있다.

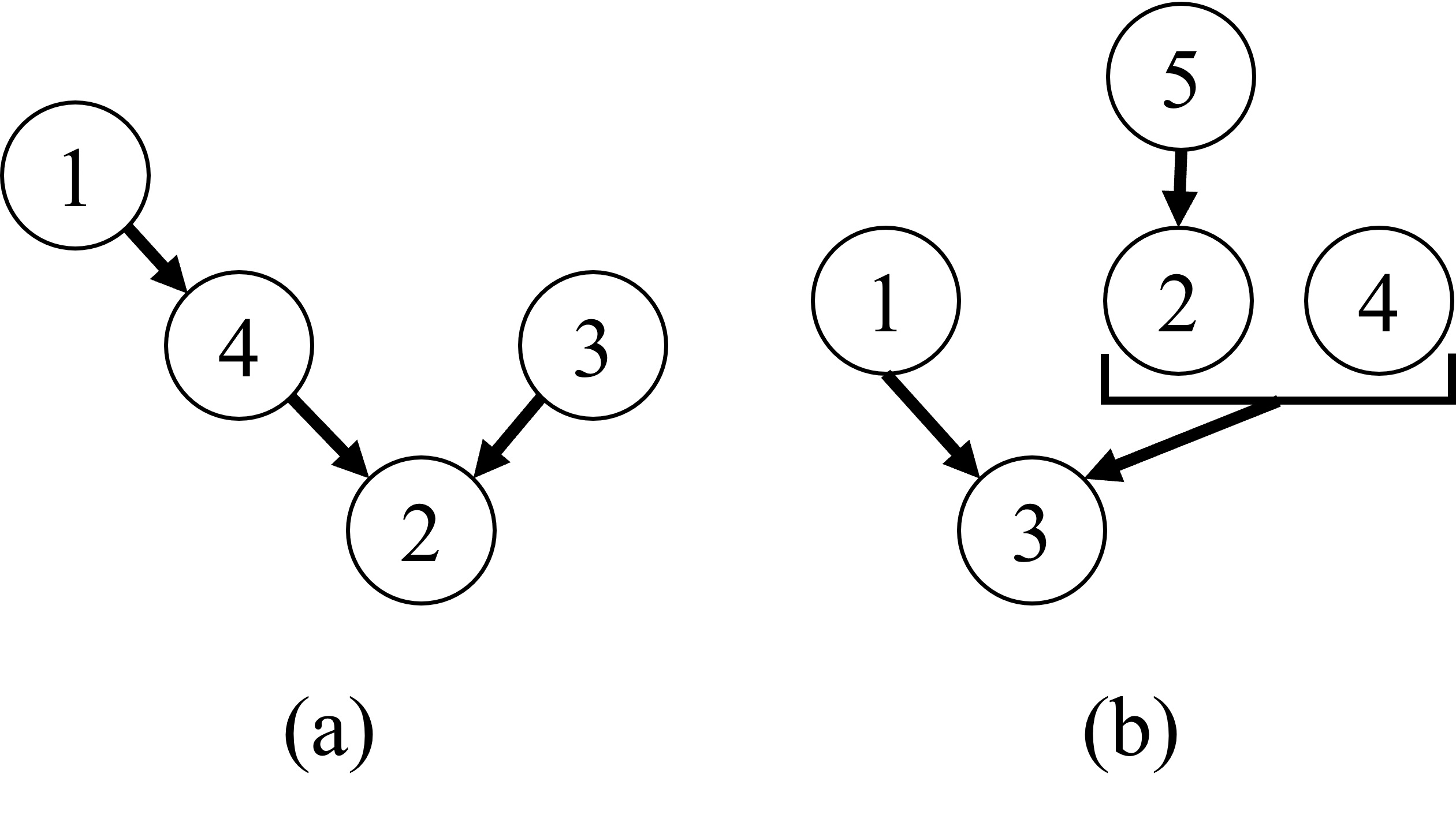
Fig.3 Examples of the complex logic diagram

추리에 있어서 문제들

다양한 논리적 퀴즈들에 대해서 다양한 문제 풀이 방법들이 있다. 예를 들면 거짓말쟁이 퀴즈가 있다.

A, B, C, D 중 거짓말을 하는 사람은 단 한 명 있다. 누가 거짓말을 하는 지 알아보자.
A: B 또는 C가 거짓말을 하고 있어.
B: 나는 거짓말을 하지 않아.
C: A는 거짓말을 하고 있어.
D: A 또는 B가 거짓말을 하고 있어.

이와 같은 논리 퀴즈에서는 표를 작성하여 각 사람이 거짓말을 하는 경우의 가짓수를 확인하는 것이 도움이 될 때가 있다.

이와 같이 여러 명제들 사이에서 결론을 추리하기 위한 수단에는 다양하고 효과적인 수단이 있을 수 있다. 본 책에서는 위와 같은 몇 가지 수단만을 다루는데, 상세한 내용은 다른 책을 참고해야 할 듯 싶다.

---

참고문헌

1 Copi, I. M., 논리학 입문, 박만준, 윤진각, Transl., Seoul, S.Korea: 경문사, 2015.