Intensity normalization of sidescan sonar imagery
Fig.1 Intensity normalization of sidescan sonar imagery
Published in: 2016 Sixth International Conference on Image Processing Theory, Tools and Applications (IPTA)
Date of Conference: 12-15 December 2016
DOI: 10.1109/IPTA.2016.7820967
내용
사이드 스캔 소나 데이터를 normalization하는 과정에서 MIxed exponential Regression Analysis (MIRA) 를 제시하고, Dark Channel Prior Method (DCP)를 사용하는 논문
MIRA
MIRA는 다음과 같은 모델 eqn.을 사용해 4개 params.를 커브 피팅하여 소나 신호를 보정한다.
\begin{equation} f(z) = ae^{bz}+ce^{dz} \end{equation}
소나 이미지의 전체 핑에 대해서 수행하지는 않고, 임의의 핑 데이터 하나에 대해서만 커브 피팅을 수행했다. Computational complexity는 $O(N)$이다.
DCP
\begin{equation} I(x) = J(x)t(x) + A(1-t(x)) \end{equation}
$I$는 관측된 이미지observed intensity, $J$는 haze가 없는 이상적인 이미지scene radiance, $A$는 대기에 의한 빛global atmospheric light, 그리고 $t$는 대기 투과율medium transmission이다.
$t$ 의 계산은 wave equation의 absorption처럼 $t(x) = e^{-\beta d(x)} $로, $\beta$는 대기의 산란계수scattering coefficient, $d$는 depth이다.
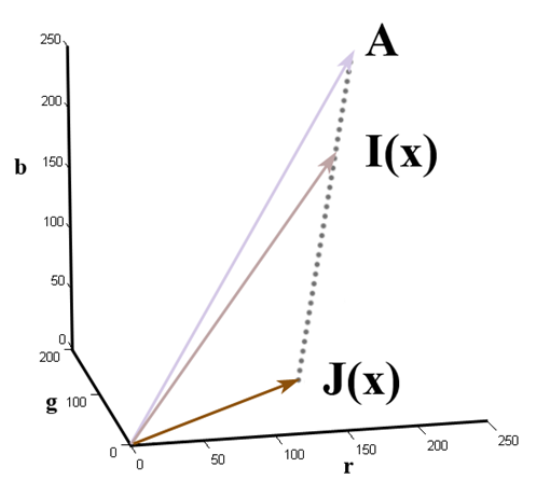
Fig.2 Haze image formation model
위 식을 다시 보면 $I$는 $J$와 $A$의 1 거리 사이의 $t$만큼의 interpolation point라고 볼 수 있다. 때문에 $t$는 다음과 같이 계산할 수 있다.
\begin{equation} t(x) = \frac{||A-I(x)||}{||A-J(x)||} \end{equation}
하지만 식은 하나인데 $I$만 알고 $J$와 $t$를 모르니 이 정보만으로는 dehazing을 할 수 없다. 때문에 DCP에서는 다음과 같은 조건을 추가한다. Haze-free image(즉, $J$)의 하늘이 아닌 픽셀은 RGB 채널 중 하나의 값이 매우 낮다는 것이다. 이 채널을 다크 채널Dark channel이라고 하면 다음과 같이 쓸 수 있다.
\begin{equation} J^{dark}(x) = \min _{c \in {r,g,b} }( \min _{y \in \Omega (x)}(J^c(y))) \end{equation}
원 논문에서는 이 식을 기반으로 $t$를 구하게 되는데, 하지만 본인이 수행하는 소나 이미지는 흑백 이미지이기 때문에 이 특별히 값이 낮은 채널이 존재하지 않는다. 즉, dark channel image가 소나 이미지 그 자체로 생성되게 되고, local patch $\Omega$의 local maximum 값으로 normalize한 이미지가 나올 것임을 생각해 볼 수 있겠다. 즉, 소나 이미지에는 DCP로 dehazing을 수행하기 어렵다는 결론을 낼 수 있겠다.
Structural similarity index measure
Structural similarity index measure(SSIM)은 본 논문에서 SSS로 특정 랜드마크를 좌현 및 우현 방향에서 스캔한 이미지를 비교하기 위해 사용한 방법이다.
먼저 이미지 일부의 mean과 variance를 계산한다.
\begin{equation} \mu_x = \frac{1}{N} \sum_{i=1}^{N}{x_i} \end{equation}
\begin{equation} \sigma_x = \frac{1}{N-1} \left( \sum_{i=1}^{N}{ (x_i - \mu_x)^2 } \right)^{\frac{1}{2}} \end{equation}
두 신호 $x$와 $y$ 사이의 covariance는 다음과 같다.
\begin{equation} \sigma_{xy} = \frac{1}{N-1} \sum_{i=1}^{N}{ (x_i - \mu_x) (y_i - \mu_y) } \end{equation}
Comparison function을 다음과 같이 정의한다.
\begin{equation} L(a,b) = \frac{2ab}{a^2 + b^2} \end{equation}
그러면, SSIM은 다음과 같이 정의한다. 각각 luminance comparison, contrast comparison, 그리고 structure comparison이다.
\begin{equation} SSIM(x,y) = L(\mu_x, \mu_y)L(\sigma_x, \sigma_y)s(x,y) \end{equation}
$s(x,y) = \sigma_{xy} / \sigma_x \sigma_y $ 이다.
Sonar Image Quality Assessment Metric
Sonar Image Quality Assessment Metric (SIQEM)은 본 논문에서 SSS의 이미지 퀄리티를 확인하기 위해 새롭게 제안한 방법이다. 먼저 이미지를 $M \times N$개의 패치로 나눈 후, 각 $m,n$번째 패치에 대해 mean intensity $ \mu_{m,n} $를 계산한다. 그리고 인접한 패치의 mean intensity $\mu_{m_k,n_k}$와 비교하여 $\mu_{m,n}$ 으로 나눈다. 즉 다음 식과 같다. 본문에서는 Weber’s perceptual law를 사용했다고 한다.
\begin{equation} C_{m,n} = \frac{\rm{max}(\mu_{m,n} - \mu_{m_k,n_k})}{\mu_{m,n}} \end{equation}
\begin{equation} SIQEM(S) = \frac{1}{M} \frac{1}{N} \sum_{m=1}^{M}{ \sum_{n=1}^{N}{C_{m,n}} } \end{equation}
값이 낮을수록 이미지 퀄리티가 높은 지수라고 한다.
식을 봐서는 이미지를 직사각형 구획으로 구분하여, 각 구획별 큰 변화가 없을 경우 그 값이 낮을 것으로 예상된다.
생각
Computational complexity가 $O(N)$ 인건, 한 ping에 대해서만 curve fitting 계수를 계산하고 그걸 SSS data에 1-D loop를 수행해서 그런 것 같다. 나도 비슷하게 한 data에만 curve fitting을 하고 계산해 보자.
Todo
-
MIRA 코드 작성
-
SSIM 예시 코드 실행
-
SIQEM 코드 작성
참고문헌
M. S. Al-Rawi et al., “Intensity normalization of sidescan sonar imagery,” 2016 Sixth International Conference on Image Processing Theory, Tools and Applications (IPTA), Oulu, Finland, 2016, pp. 1-6, doi: 10.1109/IPTA.2016.7820967.
https://hyeongminlee.github.io/post/pr001_dehazing/
K. He, J. Sun and X. Tang, “Single Image Haze Removal Using Dark Channel Prior,” in IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 33, no. 12, pp. 2341-2353, Dec. 2011, doi: 10.1109/TPAMI.2010.168.

Leave a comment